 Green
GreenДопоможіть будь ласка ДАМ 48 БАЛІВ
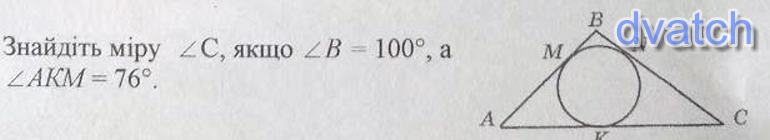
ответы: 1
Зарегистрируйтесь, чтобы добавить ответ
Ответ:
В треугольник АВС вписана окружность. Точки касания на АВ – М, на ВС – N, на АС – К. Найдите угол C треугольника АВС, если угол В = 100°, а угол АКМ = 76°.
: 52°
Объяснение:
а) АМ=АК - равные отрезки касательных из одной точки. ⇒
∆ АКМ - равнобедренный, ∠ АМК=∠АКМ=76°
Тогда из суммы углов треугольника в ∆ АКМ ∠ А=180°-2•76=28°
Из суммы углов треугольника в ∆ АВС ∠С=180°-100°-28°=52°
Или:
Из развернутых углов АМВ и АКС ∠ВМК=∠СКМ=180°-76°=104°
Сумма углов выпуклого четырехугольника 360°. ⇒
В четырёхугольнике ВМКС ∠ С=360°-100°-2•104°=52° - (он же угол ∆ АВС)
185
 Sherri
SherriЧтобы ответить необходимо зарегистрироваться.