посчитайте, Вычислить определенный интеграл с точностью α = 0,001, представив подынтегральную функцию в виде степенного ряда

Question

Алгебра

Blanchard

3 year(s) ago

посчитайте, Вычислить определенный интеграл с точностью α = 0,001, представив подынтегральную функцию в виде степенного ряда

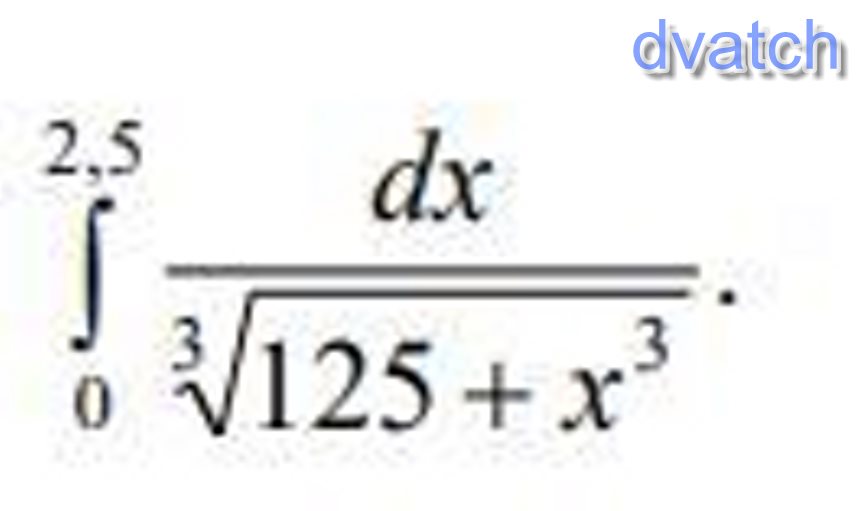
ответы: 1

Зарегистрируйтесь, чтобы добавить ответ

Ответ:

$0. 495$

Преобразуем интеграл: $$intlimit_0^{2. 5}dfrac{dx}{sqrt[3]{125+x^3}}=left[t=dfrac{x}{5}right]=intlimit_0^{0. 5}dfrac{dt}{sqrt[3]{1+t^3}}=(*)$

Известное разложение: $(1+t)^alpha=1+sumlimits_{n=1}^infty left(prodlimits_{k=1}^n dfrac{alpha-k+1}{k} right)cdot x^n ;;;;forall alpha, x:|x|<1$

В частности, имеем $dfrac{1}{sqrt[3]{1+t}}=1+sumlimits_{n=1}^infty left(prodlimits_{k=1}^n dfrac{-frac{1}{3}-k+1}{k} right)cdot t^n$ .

Тогда $$(*)=intlimit_0^{0. 5}left(1+sumlimits_{n=1}^infty left(prodlimits_{k=1}^n dfrac{-frac{1}{3}-k+1}{k} right)cdot t^{3n}right)dt=(**)$

Меняем интегрирование и суммирование местами:

$$(**)=0. 5-0+sumlimits_{n=1}^infty left(prodlimits_{k=1}^n dfrac{-frac{1}{3}-k+1}{k} right)intlimit_0^{0. 5} t^{3n}dt=(***)$

$$intlimit_0^{0. 5} t^{3n}dt=left. left(dfrac{t^{3n+1}}{3n+1}right)right |limits_0^{0. 5}=dfrac{1}{(3n+1)cdot 2^{3n+1}}$

Значит,

$$(***)=0. 5+sumlimits_{n=1}^infty underbrace{left(prodlimits_{k=1}^n dfrac{-frac{1}{3}-k+1}{k} right)dfrac{1}{(3n+1)cdot 2^{3n+1}}}_{a_n}=(****)$

$a_1=left(dfrac{-frac{1}{3}-1+1}{1} right)dfrac{1}{(3+1)cdot 2^{3+1}}=-dfrac{1}{3} cdot dfrac{1}{2^6}$

$a_2=left(dfrac{-frac{1}{3}-1+1}{1} right)left(dfrac{-frac{1}{3}-2+1}{2} right)dfrac{1}{(6+1)cdot 2^{6+1}}=dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{7cdot 2^{6}}Rightarrow \ Rightarrow |a_2|=dfrac{1}{126cdot 32}<dfrac{1}{100cdot 10}=0. 001$

Значит, для указанной точности члены разложения с номерами $ngeq 2$ можно отбросить. Тогда, с указанной точностью,

$(****)approx0. 5-dfrac{1}{3} cdot dfrac{1}{2^6}approx 0. 5-0. 005=0. 495$

379

Tulabar

Oct 20, 2021

посчитайте, Вычислить определенный интеграл с точностью α = 0,001, представив подынтегральную функцию в виде степенного ряда

Другие вопросы: - Алгебра