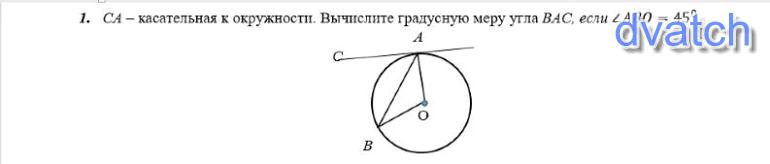
CA-Касательная к окружности. Вычеслите градусную меру угла BAC Если угол ABO=45 градусов

Рассмотрим ∆АОВ. Он равнобедренный, т. к. ОВ=АО как радиусы. Значит <ОАВ=<АВО=45° (углы при основании равны)

Т. к. радиус перпендикулярен касательной в точке касания, то <OAC=90°

<ОАС=<АВО+<ВАС, отсюда

<ВАС=<ОАС-<АВО

<ВАС=90-45=45°

<ВАС=45°

: 45°