посчитайте ❗Даю 24 бала​

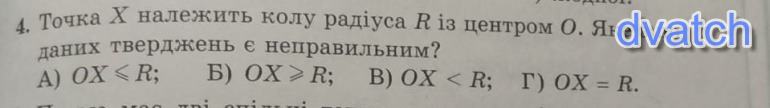
Б)

Задание

Точка Х принадлежит кругу радиуса R с центром О. Какое из представленных утверждений является неправильным?

А) ОХ ≤ R

Б) ОХ ≥ R

В) ОХ < R

Г) ОХ = R

Решение

Сначала дадим определения круга и окружности.

Круг — множество точек плоскости, удаленных от заданной точки этой плоскости (центр круга О) на расстояние, не превышающее заданное (радиус круга) R.

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая; это граница круга.

Рассмотрим, каких из предложенных утверждений соствуют (либо не соствуют) определению круга.

А) ОХ ≤ R - это верное утверждение, так как оно целиком и полностью соствует определению круга: расстояние ОХ не превышает радиуса.

Б) ОХ ≥ R - это ошибочное утверждение, так как ОХ не может быть больше радиуса.

В) ОХ < R - данное утверждение является верным, но неполным: оно не учитывает те точки, которые лежат на окружности;

Г) ОХ = R - данное утверждение является верным, но неполным: оно учитывает только те точки, которые лежат на окружности, и не учитывает точки, которые лежат между центром окружности и её границей.

ВЫВОД: так как в Задании спрашивается какое (то есть только одно какое-то) утверждение является неправильным, то укажем только одно утверждение Б), которое явно является неправильным. При этом, как было отмечено в решении, утверждения В) и Г) являются неполными, так как охватывают какие-то, но не все области правильных значений, поэтому, строго говоря, и их тоже надо было бы отнести к неправильным.

: Б)