посчитайте кто знает мне оооооооочень ​

См. Объяснение

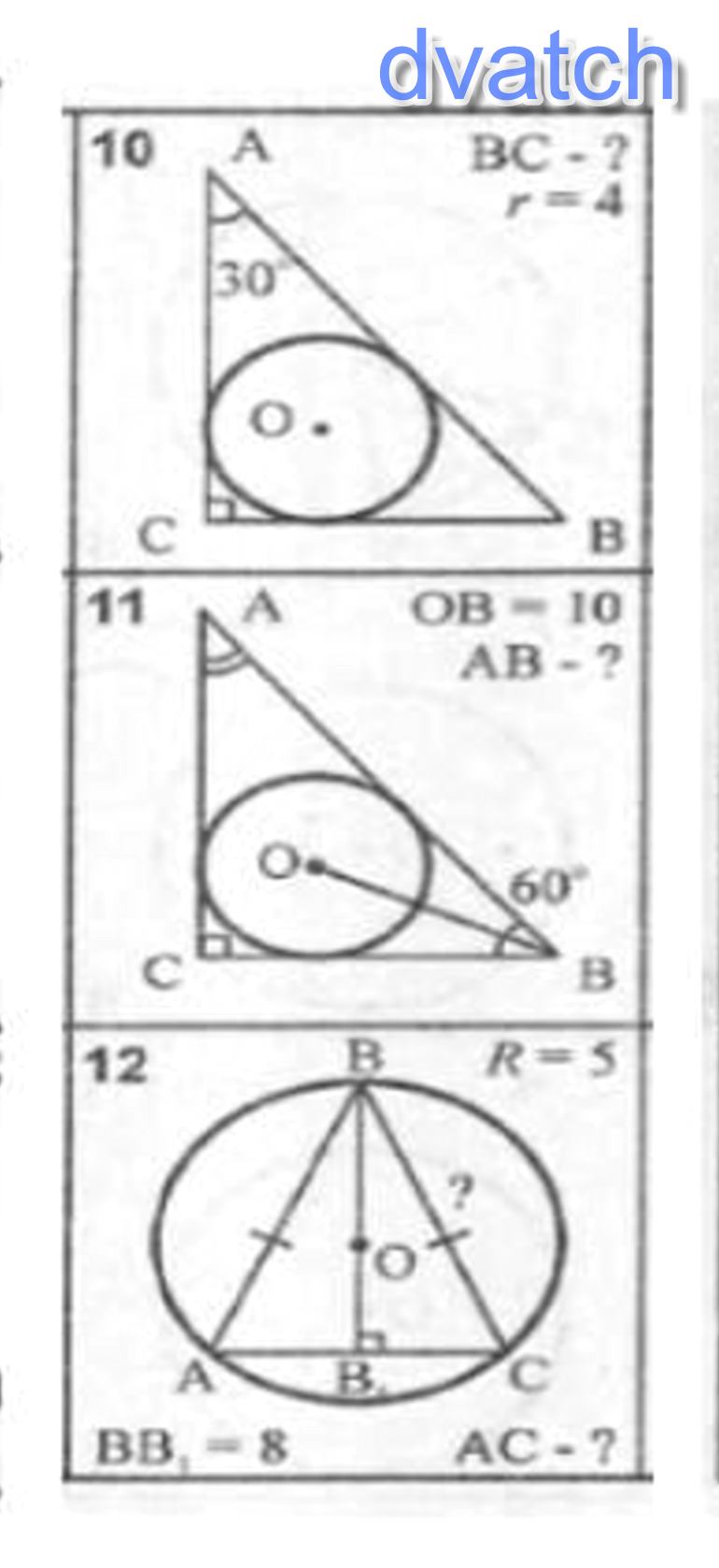
№ 12

Так как АО = ОВ = ОС = R = 5, то

ОВ₁ = ВВ₁ - ОВ = 8-5=3

АВ₁ = √(АО²- ОВ₁²) = √(5²-3²) = √(25-9) = √16 = 4

Так как высота равнобедренного треугольника, проведённая к его основанию, является его медианой, то:

АС = 2·АВ₁ =2·4 =8

: АС = 8

ПРИМЕЧАНИЕ

Решение №№ 10 и 11 даю повторно:

№ 10

1) Согласно теореме о длине окружности, вписанной в прямоугольный треугольник: диаметр D окружности, вписанной в прямоугольный треугольник, равен сумме длин катетов минус длина гипотенузы:

D = AC + ВС - АВ,

где D = 2r = 2 · 4 = 8

AC + ВС - АВ = 8 (1)

2) Пусть гипотенуза АВ = х, тогда

катет ВС = 0,5АВ = 0,5х (катет, лежащий против угла 30°, равен половине гипотенузы);

катет АС = х · cos30° = x√3/2 (катет равен гипотенузе, умноженной на косинус угла, прилежащего к этому катету).

3) Таким образом, выражение (1) можно записать в виде:

x√3/2 + 0,5х - х = 8

х√3/2 - 0,5х = 8

х(√3/2 - 0,5) = 8

х·((√3 - 1)/2) = 8

х = 16/(√3 - 1)

АВ = 16/(√3 - 1)

4) ВС = 0,5 АВ = (16/(√3 - 1))/2 = 8/(√3 - 1) ≈ 8 : (1,732 -1) ≈ 8 : 0,732 ≈ 10,93

: ВС = 8/(√3 - 1) ≈ 10,93

№ 11

1) Опустим перпендикуляр из точки О на сторону ВС и обозначим его OF; OF является также радиусом окружности, вписанной в треугольник АВС. В прямоугольном треугольнике BFO (угол F - прямой) катет OF, лежит против угла OВF.

2) Согласно условию задачи, ∠ОВС = ∠ОВА = 60° : 2 = 30°.

Катет, лежащий против угла 30°, равен половине гипотенузы:

OF = 0,5 ОВ = 10 · 0,5 = 5

Таким образом, радиус окружности, вписанной в прямоугольный треугольник АВС, равен 5, а диаметр D этой окружности равен:

D = 2r = 2 · 5 = 10

3) Согласно теореме о длине окружности, вписанной в прямоугольный треугольник: диаметр D окружности, вписанной в прямоугольный треугольник, равен сумме длин катетов минус длина гипотенузы:

D = AC + ВС - АВ,

AC + ВС - АВ = 10 (1)

4) В прямоугольном треугольнике АВС (угол С - прямой):

∠А = 90° - ∠В = 90° - 60° = 30°

5) Пусть гипотенуза АВ = х, тогда катет ВС = 0,5АВ = 0,5х (катет, лежащий против угла 30°, равен половине гипотенузы);

катет АС = х · cos30° = x√3/2 (катет равен гипотенузе, умноженной на косинус угла, прилежащего к этому катету).

6) Таким образом, выражение (1) можно записать в виде:

x√3/2 + 0,5х - х = 10

х√3/2 - 0,5х = 10

х(√3/2 - 0,5) = 10

х·((√3 - 1)/2) = 10

х = 20/(√3 - 1)

АВ = 20/(√3 - 1) ≈ 20 : (1,732 -1) ≈ 20 : 0,732 ≈ 27,32

: АВ = 20/(√3 - 1) ≈ 27,32