LukillДано, что в тетраэдре DABC ребро DB перпендикулярно ребру AC. На рёбрах DA и DC расположены серединные точки M и N. Докажи, что DB перпендикулярно MN. 1. Так как M и N — серединные точки DA и DC, то MN (вставить) треугольника ACD. 2. Средняя линия (вставить) третьей стороне треугольника, то есть AC. 3. Если DB перпендикулярна одной из (вставить) прямых, то она (вставить) и другой прямой.
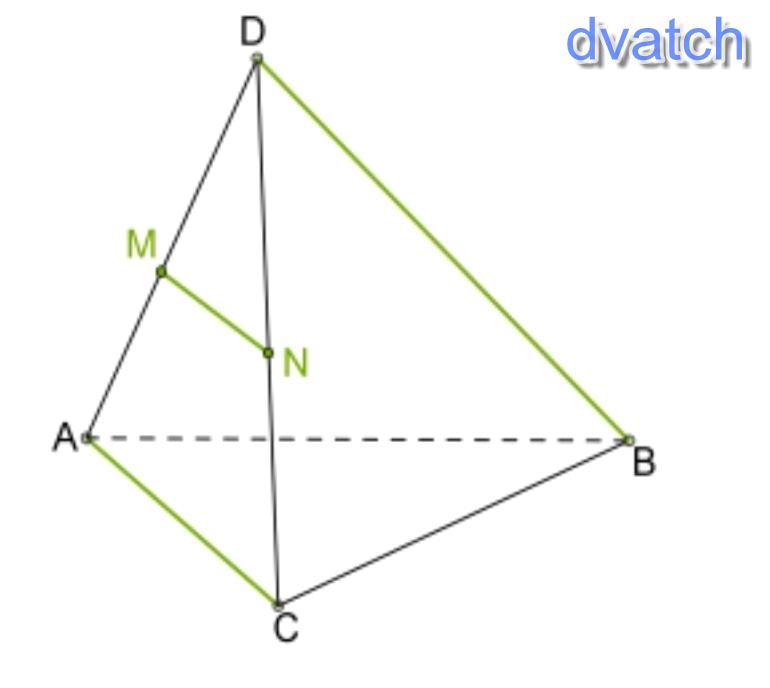
ответы: 1
Зарегистрируйтесь, чтобы добавить ответ
Ответ:
Відповідь:
Пояснення:
1. MN средняя линия △АСD
2. паралельна. . . . АС
3. из паралельних прямих, то она перпендикулярна и второй
211
Michael WilliamsЧтобы ответить необходимо зарегистрироваться.
