посчитайте , даю 30 Поинтов​

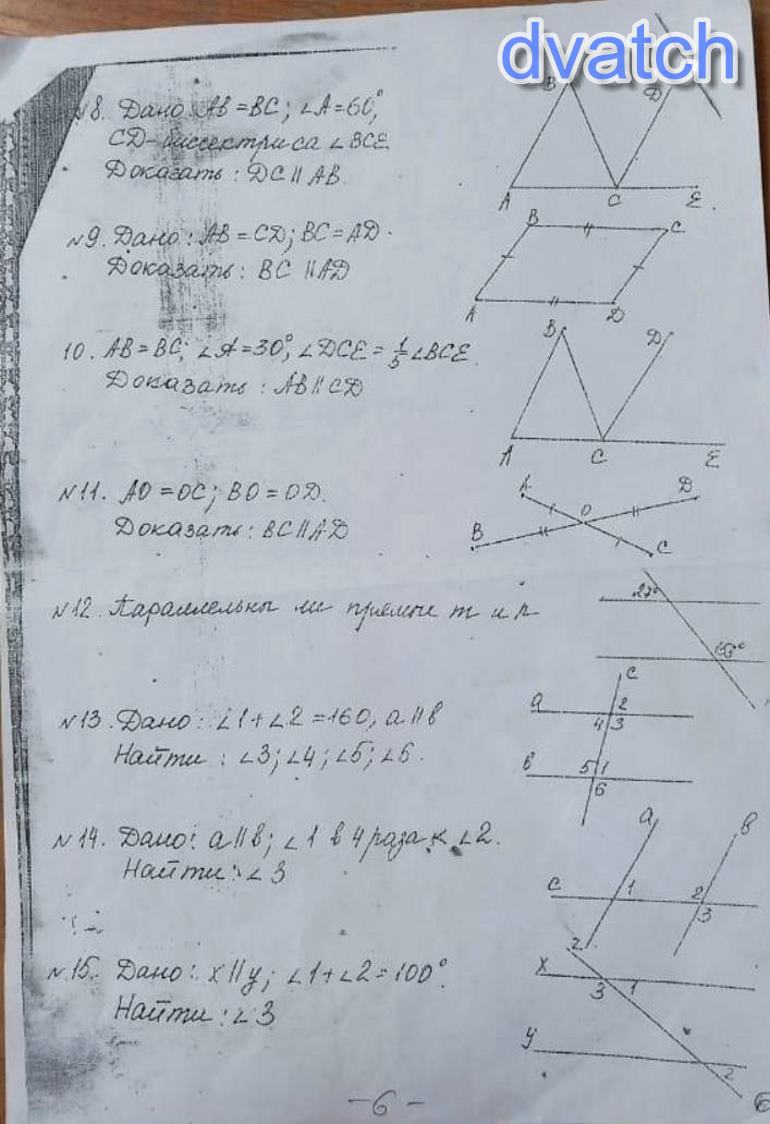
8. если АВ=ВС значит треугольник равнобедренный,а у равнобедренного треугольника углы при основании равны, значит угол А равен угол С равен углу В (180-60-60=60) равен 60 . следовательно ВСЕ =180-60=120градус. а ДСЕ-60. значит АВ паралельно ВС.

9.

теорема :если в четырехугольнике противоположные попарно равны то четырехугольник параллелограмм. А у параллелограмма противоположные стороны паралельны,другой способ треугольни АВС=треугольник АСД по трем сторонам ,АД=ВС,АВ=СД. АС-общая,угол САД=угол АСВ-это внутренные разносторонныеьуглы . Если при пересечении двух прямых третьей внутренные разносторонныеьуглы ровно то прямые паралельны.

10.

АВ=ВС, значит треугольник равнобедренный и угол А = углу ВСА=30

Угол В =180-30-30=120°

Угол ВСА смежный с ВСЕ, значит ВСЕ=150°( смежные углы в + = 180°)

DCE=1/5BCE

BCE=150

DCE=30

Угол ВАС=DCE=30° значит прямые //( если соотв углы =, то прямые //)

11

. 1) Рассмотрим треугольники BOA и COD.

1. AO=OC (по условию )

2. BO= OD (по условию)

3. Угол BOA =углу COD(вертикальные)

Треугольники равны по двум сторонам и углу между ними.

2)угол ABO = углу CDO(BD секущая, накрест лежащие).

AB параллельна СD по п. 2.

ч. т. д.

13.

Дано: a || b, с - секущая, ∠1+∠2=160°.

Найти: ∠3, ∠4, ∠5, ∠6.

∠1=∠2 - как соственные углы при параллельных прямых a и b и секущей c

∠1=∠2 = (∠1+∠2)/2 = 160°/2 = 80°

∠2=∠4=80° - как вертикальные углы

∠2 и ∠3 - смежные углы

Сумма смежных углов равна 180°:

∠2+∠3=180°

∠3 = 180° - ∠2 = 180° - 80° = 100°

∠3=∠5 - как накрест лежащие углы при параллельных прямых a и b и секущей c

∠3=∠5=100°

∠5=∠6=100° - как вертикальные углы

: ∠3=100°, ∠4=80°, ∠5=100°, ∠6=100°.

14.

Т. к. а паралельно б то при секущей с,угол 1 и угол 2-одностронние. Пусть х-угол 1 тогда угол 2-4 х. Известно что сумма односторонних углов равно 180. Решим:х+4х=180

5х=180

х=36-угол 1

угол 1=угол 3=36гр.

15.

угол 1 равен угол 2(соственные)

угол 1 рвно угол 3 (смежные)

180-50=130-угол 3