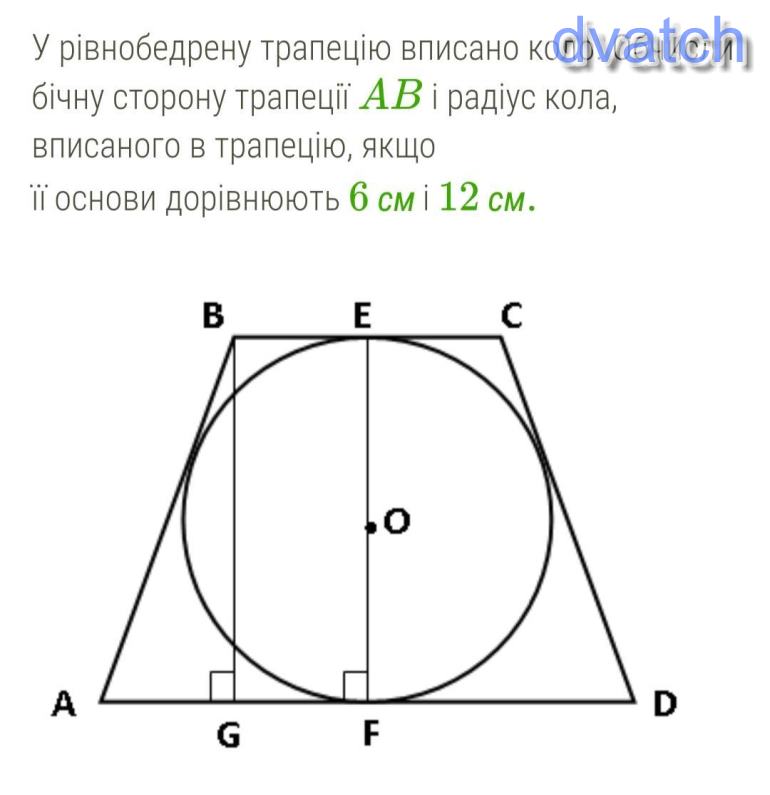
У рівнобедрену трапецію вписано коло. Обчисли бічну сторону трапеції AB і радіус кола, вписаного в трапецію, якщо її основи дорівнюють 6 см і 12 см.

АВ=9см

ОЕ=3√2см

Дано

ABCD- равнобокая трапеция

ВС=6см

АD=12см

О- центр вписанной окружности.

АВ=?

ЕО=?

_____

Решение.

В трапецию можно вписать окружность когда сумма основании равна сумме боковых сторон.

ВС+AD=AB+CD

AB=CD.

AB+CD=6+12=18см

АВ=18/2=9см.

Проведём высоту СМ.

АG=MD

AG=(AD-BC)/2=(12-6)/2=6/2=3см

∆АВG- прямоугольный треугольник

По теореме Пифагора

ВG=√(AB²-AG²)=√(9²-3²)=√(81-9)=

=√72=6√2 см

Высота трапеции равна диаметру окружности.

BG=EF=6√2см.

ОЕ=BG/2=6√2/2=3√2см