даю 20 поинтов. посчитайте сделать это. ​

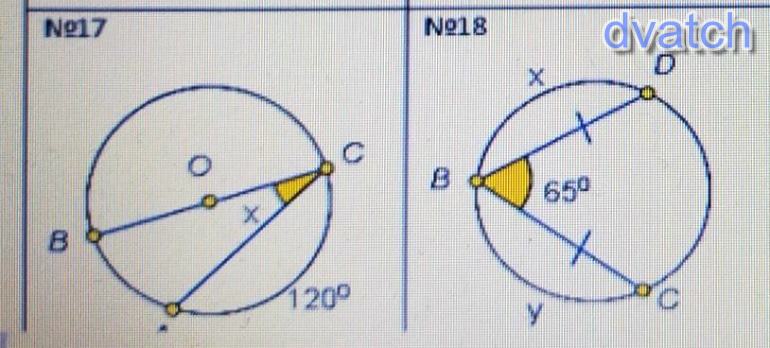
№1

Проведем прямую АО, которая является радиусом. Тогда АО = ОС, а значит, ΔАОС - равнобедренный.

Градусная мера дуги равна градусной мере центрального угла, то есть, ∠АОС = 120°

Т. к. ΔАОС - равнобедренный, то ∠OAC=∠OCA = (180 - 120) / 2 = 30°

: х = 30°

№2

Проведем хорду DC и получим треугольник BDC, который является равнобедренным, т. к. BD = BC

Найдем углы BDC и BCD

(180 - 65) / 2 = 57,5°

Эти углы - вписанные в окружность. Их градусная мера равна половине дуги, на которую они опираются. Отсюда узнаем градусные меры х и у:

х = у = 57,5 * 2 = 115°

: 115°