Найдите решение . Мне нужны все, кроме 82 и 84. посчитайте хотя бы 81, 83, 85. ДАЮ 90 поинтов за сть

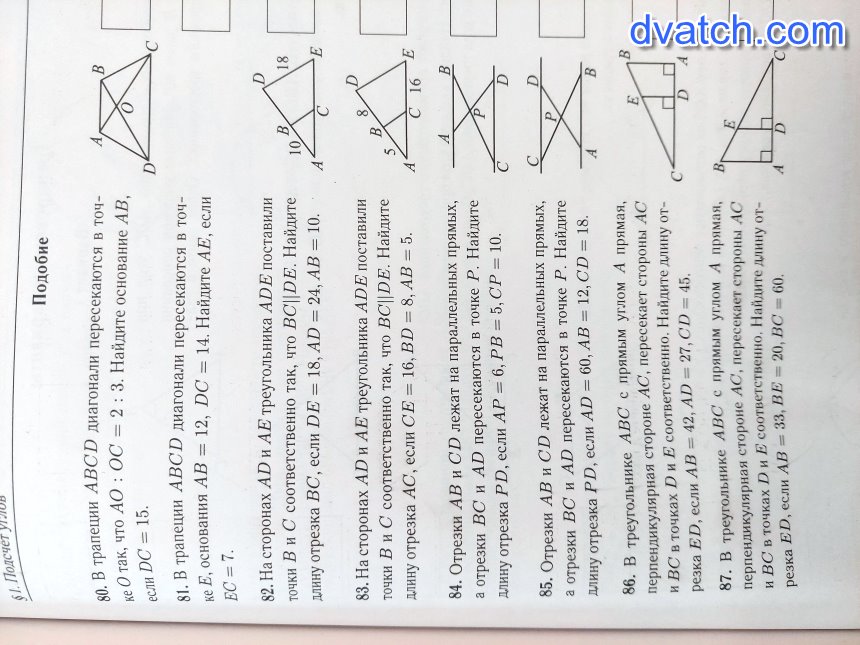
80) Треугольники AOB и COD - подобны (по двум углам, например: AOB = COD (вертикальные), ABO = CDO (накрест лежащие при параллельных прямых AB и CD)). Значит AB : CD = AO : OC = 2 : 3. Т. к. CD = 15, AB = 10.

81) Треугольники AEB и CED - подобны (см. пункт "80"). Следовательно, AB : CD = AE : EC = 12 : 14 = 6 : 7. Т. к. ЕС = 7, AE = 6.

83) Треугольники ABC и ADE - подобны (по двум углам: ABC - общий, CDA = EDA (со ственные при параллельных прямых BC и DE). Значит, AB:AD = AC:AE. Получается, что 5:13 = AC:(AC+16). Решим это уравнение: 5*AC + 5*16 = 13*AC. 8*AC = 80. AC = 10.

85) Треугольники APB и DPC - подобны (по двум углам: APB = DPC (вертикальные), ABP = DCP (накрест лежащие при параллельных прямых)). Следовательно, AB : CD = AP : PD. 12 : 18 = AP : PD. Значит,

AP : PD = 2 : 3. AP + PD = AD = 60. Значит AP = 24, PD = 36.

86) Треугольники CED и CBA - подобны (по двум углам: BCA - общий, EDC = BAC = 90). Следовательно, ED : BA = CD : CA. ED : 42 = 45 : (45 + 27). ED : 42 = 45 : 72. ED : 42 = 5 : 8. Решаем уравнение: 8 * ED = 5 * 42.

8 * ED = 210. ED = 210/8 = 26 1/4

87) Треугольники ECD и BCA - подобны (см. пункт "86"). Получается, что ED/AB = (BC-BE)/BC. ED/33 = 40/60. ED/33 = 2/3.

ED * 3 = 33 * 2. ED = 22.