 AnnaDamga
AnnaDamgaНайти производные функции
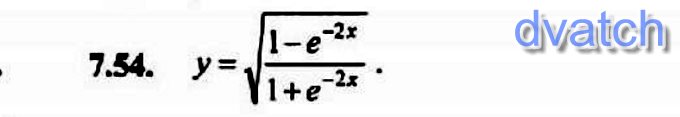
ответы: 1
Зарегистрируйтесь, чтобы добавить ответ
Ответ:
Сначала упростым выражения
f(n)=(1-e⁻²ⁿ)/(1+e⁻²ⁿ)=(e²ⁿ-1)/(e²ⁿ+1)
Теперь применим формулу (√f(x))'=0. 5f'(x)/√f(x)
Нам надо найти производную от f(n)
(e²ⁿ-1)/(e²ⁿ+1) можно ещё чуть чуть упростить
(e²ⁿ+1-2)/(e²ⁿ+1)=1 - 2/(e²ⁿ+1)
Берём производную
(1 - 2/(e²ⁿ+1))'=-2 ((e²ⁿ+1)⁻¹)'=4e²ⁿ/(e²ⁿ+1)²
Теперь
4e²ⁿ√(e²ⁿ+1)/2(e²ⁿ+1)²√(e²ⁿ-1)
219
 Vincent
VincentЧтобы ответить необходимо зарегистрироваться.