геометрия,7 классраспишите решение пож-та

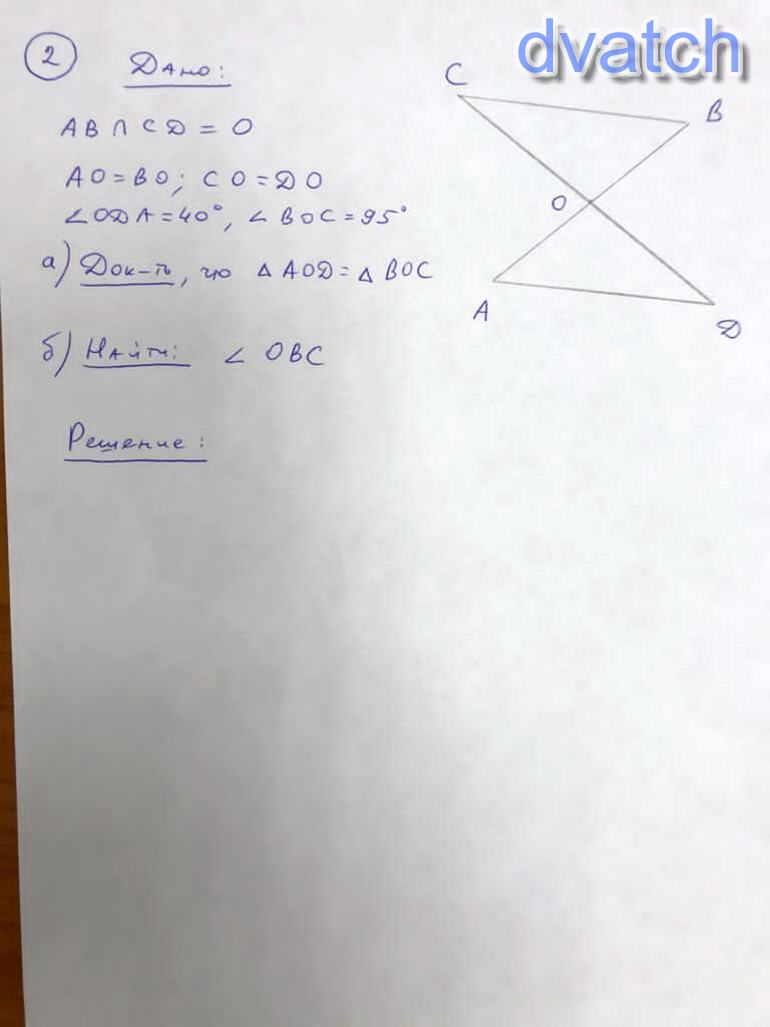
Объяснение: №1. Известно, что ∠А = 100°, а ∠С = 40°

Так как у нас имеется биссектриса, она делит угол С надвое, то есть, будут два 20° угла. Теперь найдём угол АКС через теорему суммы градусов углов треугольника. Так как сумма градусов = 180°, значит:

АКС = 180 - 100 - 20 = 60°

Так как каждая точка на прямой имеет свойство деление градусной меры надвое, делаем вывод, что градусная мера внутри треугольника АВС = 180°. У нас есть угол АКС = 60°. Угол ВКС = 180 - 60 = 120°.

Часть задачи решена

А доказательство равнобедренности ΔАВС можно доказать через теорему суммы градусов углов треугольника. У нас неизвестен угол В, он = 180 - 100 - 40 = 40°

Логично, что: если бёдра равны, равна должна быть и их траектория, если бёдра из основы были бы лучами, которые создали бы угол А. В случае, если траектория у одного из лучей иная, будет и иная град. мера у основы, так как изменяется направление луча.

Что и требовалось доказать

№2.

Доказать равенство треугольников можно через две стороны и угол между ними. Возьмём углы ВОС и АОD. Так как АО = ОВ и СО = ОD, выходит, что углы равны, так как стороны между ними одинаковы по отдельности в двух треугольниках. Что и требовалось доказать. Угол ОВС = угла ОАD, так как соотношение OB и OA равно (основы тоже равны, если судить по вышеперечисленным равенствам). Выходит, что ОСВ = ODA = 40°. Через теорему суммы градусов углов треугольника найдём ОВС: ОВС = 180 - 95 - 40 = 45°.

Вот все решения. Учись хорошо, удачи тебе

(Думаю, стоит добавить побольше баллов за старания)