посчитайте пж очень надо

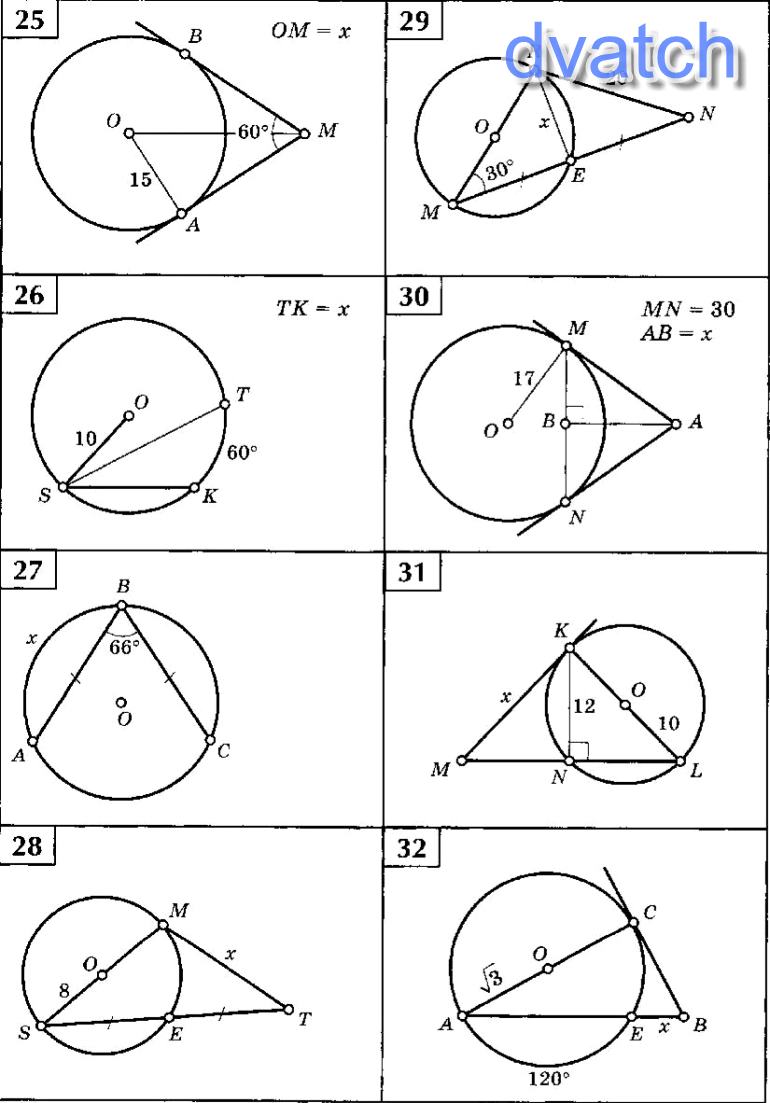
1)

∠NMO=∠NMK=30°; ∠MNO-прямой (касательная и радиус); катет, лежащий напротив угла в 30° равен половине гипотенузы=>гипотенуза MO=2NO=20

2)

1. Продолжим NO до пересечения со стороной КМ. КМ∩NO = Р;

2. О – точка пересечения высот => NP – высота ΔKMN => NP⊥КМ => ΔKPM – прямоугольный;

3. ΔKPM – прямоугольный => ∠РKN + ∠КNР = 90° (по свойству острых углов прямоугольного треугольника);

∠КNР = 90° - ∠РKN = 90° - 66° = 24°;

∠КNР = ∠FNO = 24°

5)

1. QM, BT – медианы => QO : OM = BO : OT = 2 : 1 (по свойству медиан треугольника);

2. QO : OM = 2 : 1, QM = 9 => QO = 2OM, QM = 3OM =>

OM = 9 : 3 = 3, QO = 9 – 3 = 6;

3. BO : OT = 2 : 1, BT = 12 => BO = 2OT, BT = 3OT =>

OT = 12 : 3 = 4, BO = 12 – 4 = 8;

4. QM⊥BT => ΔBOQ – прямоугольный => SBOQ = QO*BO=*6*8=24

6)

ΔРОR, в нем МО - медиана и высота => треугольник равнобедренный, поэтому ОР=ОR, а в ΔОРК против угла в 30° лежит катет ОК, равный половине гипотенузы ОР, но т. к. ОР=ОR=20, значит, ОК равен половине ОR, т. е. 20/2=10

1)

1. т. к. MK=NK, то ΔMKN - равнобедренный => KE - высота и медиана=>ME=EN=20/2=10;

2. KE⊥MN => ΔKEN - прямоугольный, по теореме Пифагора:

KN²=EN²+KE²

26²=10²+EK²

EK=24

3. SΔMKN=KE*MN*=24*20*=240

4. PΔMKN=26+26+20=72 => OE=2SΔMKN/PΔMKN=2*240/72=6

2)

1. АВ = 52 см, диаметр = 16см, => радиус = 16/2 =8 см

2. Р(АВС) = АВ+ВС+АC

Радиус вписанной окружности в прямоугольный треугольник равен:

r=(ВС+АС-АВ)/2, из формулы найдём:

ВС+АС=8*2+52,

ВС+АС=68см

3. Нам известна гипотенуза и две стороны, сумма которых - 68см. Значит, периметр равен: 68+52=120см

3)

ΔMKN - прямоугольный, ∠MKN=90°; по теореме Пифагора:

NK=√(13²-24²)=√(-407) => сторона не может быть равна отрицательному числу => задача не имеет решения

4)

S=½AB*CD

CD=CO+OD

CD=AO

AO=√(AD²+OD²)

AD=½AB=6/2=3

AO=√(3²+4²)=√25=5

CO=5

CD=5+4=9

S=½6*9=27