Как всегда "С дано и решением "

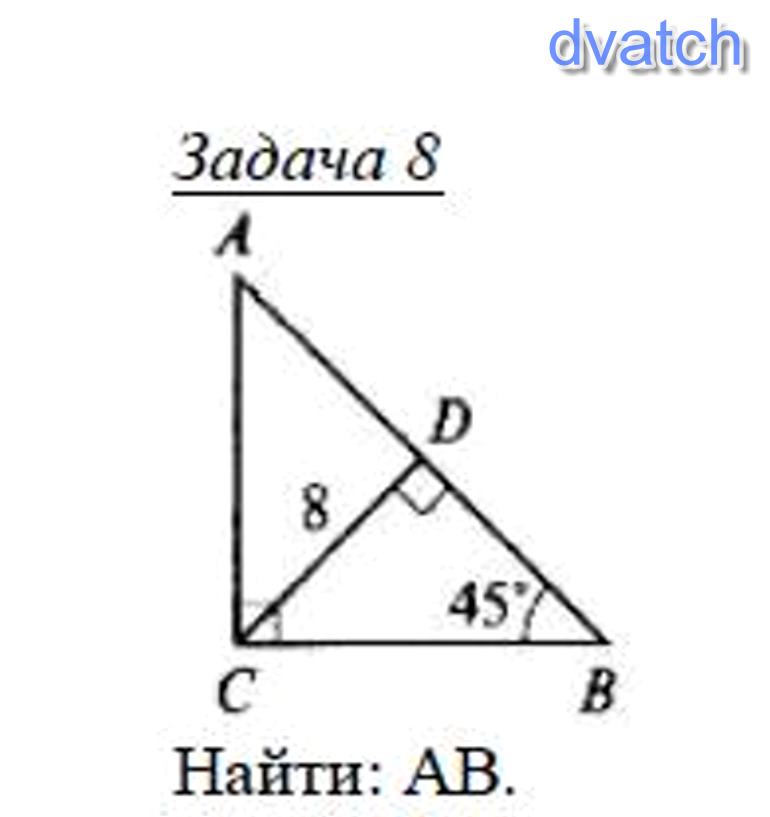
8.

Дано: CD = 8, CBD = 45°, ACB = 90°, CDB = 90°

Найти: AB

Решение: В трABC угол C=90°, угол B=45° => угол CAB=90-45=45° => трABC - равнобедренный AC=CB. Следовательно, высота CD делит AB пополам (AD=DB) и является биссектрисой => угол DCB = 90/2 = 45°. Таким образом, трCDB равнобедренный и CD=DB=8 => т. к CD медиана, то AB=AD+DB (AD=DB) => AB=2*8 = 16

: 16

7.

Дано: трABC, EC=5, BAC = 30°, BEC = 60°, BCA = 90°

Найти: AC

Решение: В трBEC cosE = 5/BE

cos60° = 5/BE

1/2 = 5/BE

BE = 10

В трABE - равнобедренный, т. к угол А = угол B = 30° (E=180-60=120°,смежный, угол В 180-120-30=30°) => BE=BA=10

AC=AE+EC=10+5=15

: 15