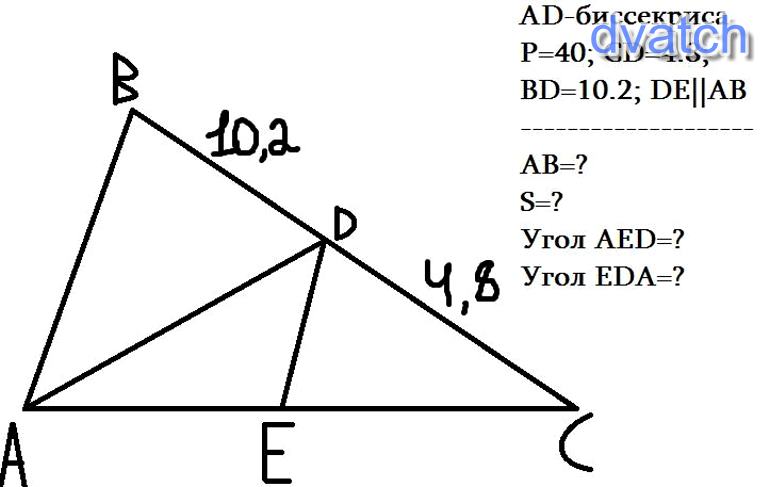
Периметр треугольника АВС 40. Из точки А провели биссектрису, которая делит сторону ВС на BD и CD соответственно с размерами 10. 2 и 4. 8. Из точки D проведён отрезок, параллельный стороне AB. Найти:1) Длину AB;2) Площадь треугольника ABC;3) Углы AED и EDA.

1) AB = 17

2) S = 60

3) ∠AED =

∠EDA =

По свойству биссектрисы

Пусть AB = 17x, AC = 8x. Тогда периметр треугольника 40 = 10,2 + 4,8 + 17х + 8х = 15 + 25х ⇒ х = 1 ⇒ AB = 17, AC = 8; BC = 10,2 + 4,8 = 15.

Заметим, что AC² + BC² = 8² + 15² = 289 = 17² = AB², то есть треугольник прямоугольный с прямым углом C по теореме, обратной теореме Пифагора. Его площадь .

∠AED = 180° - ∠CED = 180° - ∠A =

Треугольники ABC и EDC подобны по двум углам (∠C — общий, ∠A = ∠E по параллельности AB и DE).

∠EDA = ∠CDA - ∠CDE =