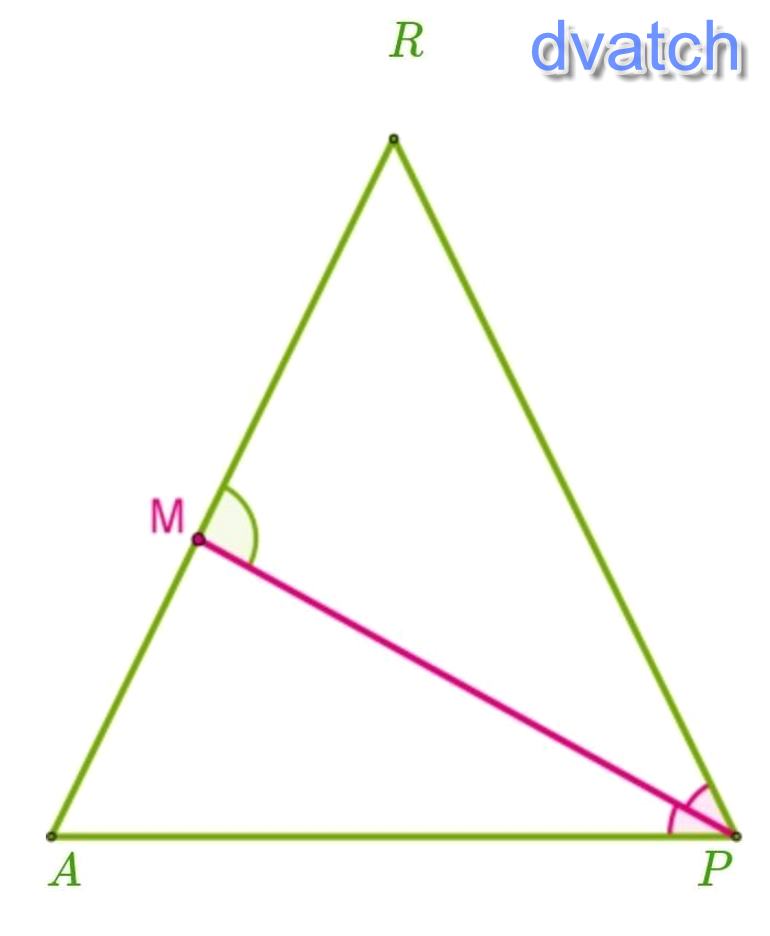
В равнобедренном треугольнике ARP проведена биссектриса PM угла P у основания AP,∡ PMR = 72°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).  ∡ A =  °; ∡ P = °; ∡ R = °. ​

. . . . . . . .

Пусть угол МРR=х, тогда угол АРR=2х.

Угол АРR=углу РАR=2х, так как у равнобедренного треугольника углы при основании равны.

Угол RMP и угол АМР-смежные. Сумма смежных углов равна 180°.

Угол АМР=180°-72°=108°

Рассмотрим треугольник АМР:

Угол АМР=108°; угол МАР=2х; угол МРА=х.

Сумма углов треугольника равна 180°

Решим с помощью уравнения:

2х+х+108=180

2х+х=180-108

3х=72

х=72:3

х=24

Угол МРА=24°

Угол МАР=2*24°=48°

Угол РАR=углу APR=48°

Как я и говорила раньше сумма углов треугольника равна 180°.

Найдём угол при вершине АRP:

Угол ARP=180°-(48°+48°)=84°