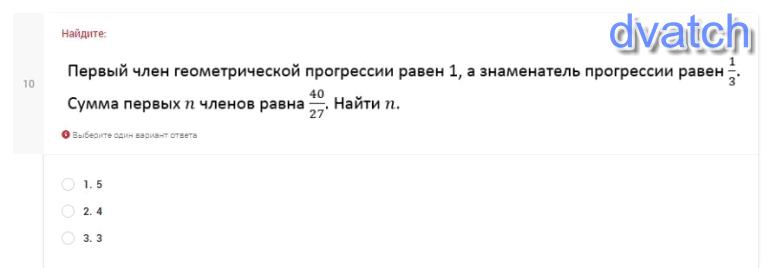
посчитайте с геометрией даю 20 поинтов

Формула суммы n-первых членов геометрической прогрессии

Sn = b1(1 - q^n)/(1 - q).

Из этой формулы трудно выделить решение относительно n.

Проще применить прямое суммирование из условия:

Любой член геометрической прогрессии можно вычислить по формуле: an=a1*q^(n-1).

S2 = 1+(1/3) = 4/3,

S3 = 1+(1/3) + (1/9) = 13/9,

S4 = 1+(1/3) + (1/9) + (1/27) = 40/27.

: n = 4.