быстрее , не знаю как решить​

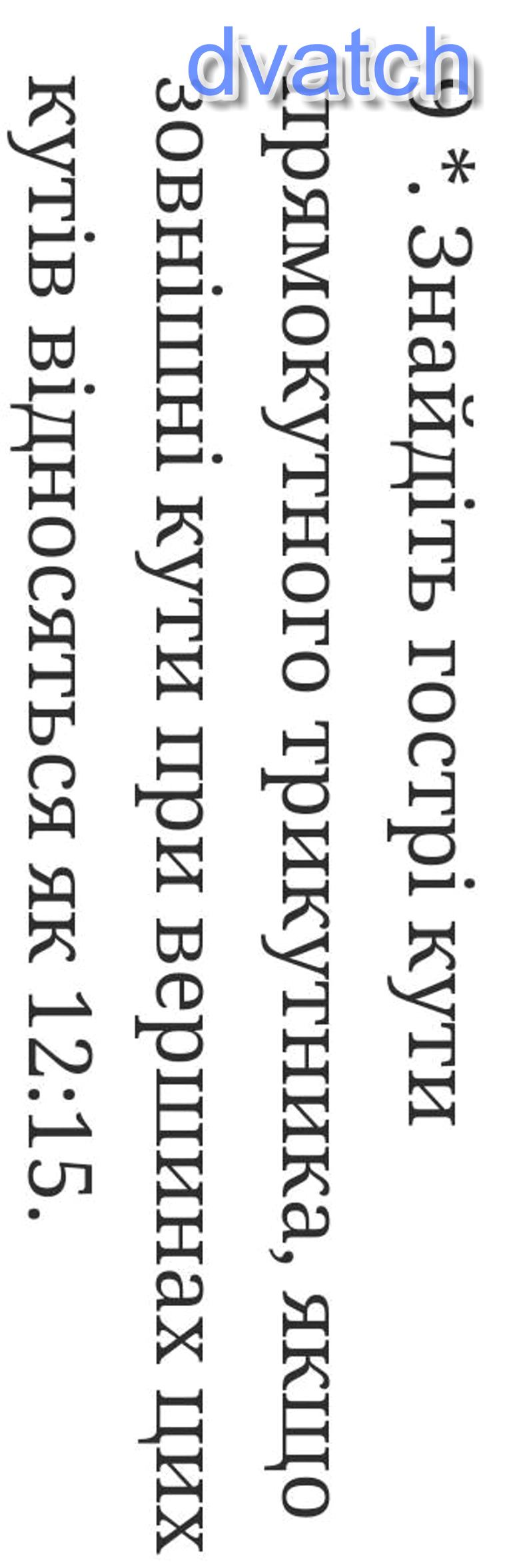
30° и 60°

Теорема: внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

Обозначим углы треугольника ∠А, ∠В и ∠С = 90°, а внешние углы 12 х и 15 х. Составим систему уравнений и найдём х:

12 х = ∠А + ∠С = ∠А + 90°

15 х = ∠В + ∠С = ∠В + 90°

или

12 х = ∠А + 90° (1)

15 х = ∠В + 90° (2)

Сложим (1) и (2)

12х + 15х = ∠А + 90° + ∠В + 90°

А так как ∠А + ∠В = 90° (сумма острых углов прямоугольного треугольника равна 90°), то:

12х + 15х = 90° + 90° + 90°

27х = 270°

х = 270 : 27 = 10°

∠12 х = 12 · 10 = 120°

∠15 х = 15 · 10 = 150°

Так как:

12 х = ∠А + 90° (1)

15 х = ∠В + 90° (2)

то заменим полученные значения 12 х на 120° и 15 х на 150° и найдём острые углы треугольника:

120° = ∠А + 90°, откуда ∠А = 120° - 90° = 30°

150° = ∠В + 90°, откуда ∠В = 150° - 90° = 60°

: 30° и 60°.