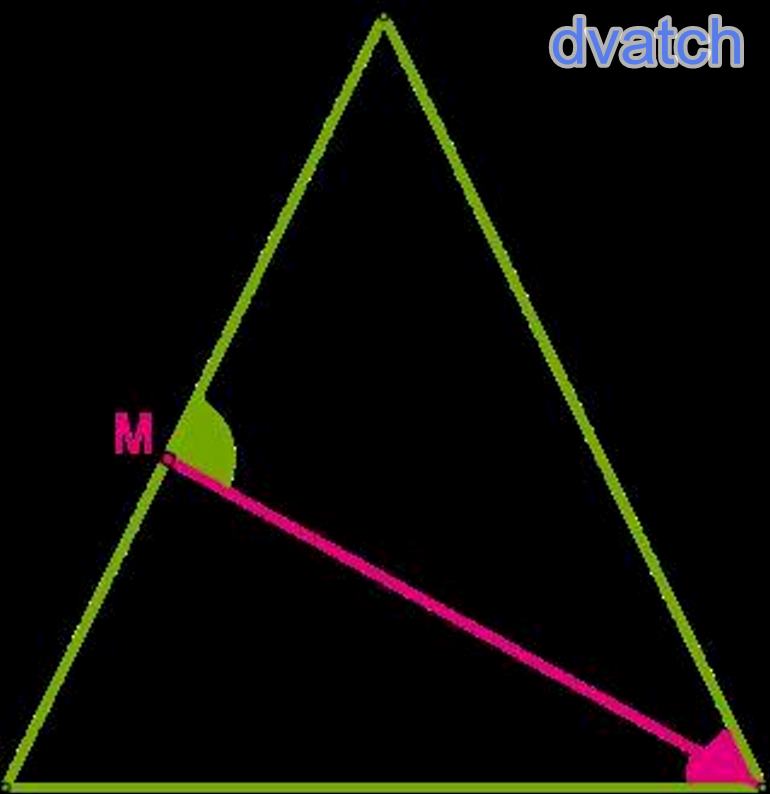
В равнобедренном треугольнике DEP проведена биссектриса PM угла P у основания DP,∡ PME = 84°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных). ∡ D = °;∡ P = °;∡ E = °.

∠D = 56°

∠P = 56°

∠Е = 68°

Дано:

Треугольник DEP

DE = PE

∠P = ∠D

∠PDE = ∠DPE = x

PM - биссектриса, то есть ∠ЕРМ = ∠DPM = 0. 5x

∠PME = 84°

Найти:

∠D - ? ∠P - ? ∠E - ?

Решение:

Расcмотрим ΔDPM

∠D = x; ∠DPM = 0. 5 x

∠PME = 84° является внешним углом для ΔDPM при вершине М

∠PME = ∠D + ∠DPM

84° = х + 0,5х

1,5х = 84°

х = 56°

Таким образом

∠D = 56°

∠P = ∠D = 56°

По свойству углов треугольник

∠Е = 180° - (∠D + ∠P) = 180° - (56° + 56°) = 68°